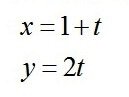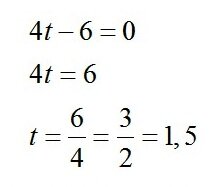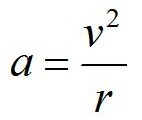|
Новая встреча с бабой ЕГЭКаждый год публикуется демовариант ЕГЭ. Но вместе с ним публикуются еще кодификатор и спецификация. Что за фигня? 1. Механика Вот, пока всё. Ознакомившись, с удовлетворением отмечаем, что всё нам в принципе знакомо, обо всём имеем кое-какое представление, ничего не пропустили. Это хорошо. Пример 1 задания А1 (взято из пособия «В.А.Грибов ЕГЭ – 2014»)
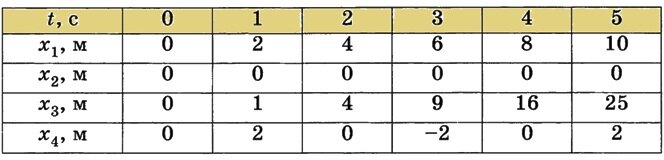
Решение. Первое тело за каждую секунду проходило 2 метра, его скорость постоянна 2 м/с; Пример 2 задания А1 (взято из пособия «В.А.Грибов ЕГЭ – 2014») Решение. Допустим, наблюдатель сидит в том автомобиле, который едет медленнее, 60 км/час. Для наблюдателя его автомобиль как бы неподвижен. Его обгоняет быстрый автомобиль. С какой скоростью он мимо него проносится? 110 – 60 = 50 км/час. Если наблюдателя посадить в быстрый автомобиль – то он сам обгонит медленный, То есть медленный мимо него будет двигаться в противоположную сторону, пятиться назад. Но МОДУЛЬ относительной скорости будет такой же. Ответ №2. Пример 3 задания А1 (взято из пособия «В.А.Грибов ЕГЭ – 2014»)
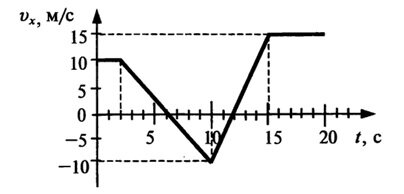
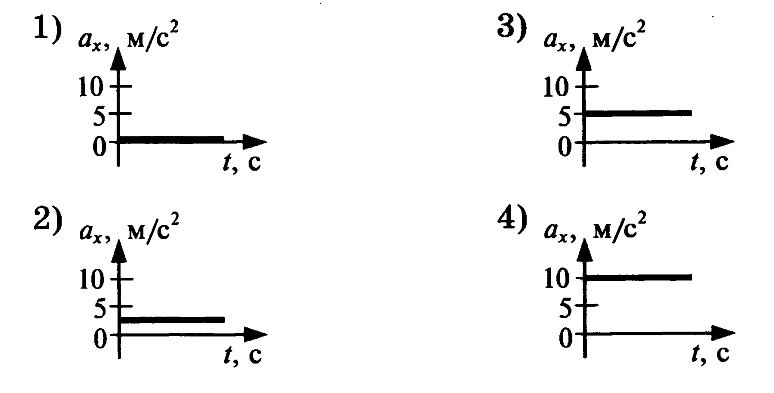
График зависимости от времени проекции ускорения этого тела ax в интервале времени от 10 до 15 секунд совпадает с графиком
Решение. Сначала обратим внимание на формулировку задания. Речь идёт о ПРОЕКЦИЯХ скорости и ускорения на ось Х. Мы разобрали выше, что движение точки в трёхмерном пространстве равноценно можно заменить движением её проекций на координатные оси. Мы не говорили – но это само собой вытекает – что можно рассматривать и проекции скорости (ускорения) на координатные оси. И вот, во многих задачках, применён такой финт. По-сути задачка простая, на движение тела по прямой линии (типа, как ехал поезд от вокзала), но подаётся это, как движение вдоль одной из координатных осей. Надо это твёрдо иметь в виду и не паниковать от умных слов «проекция vx». 15 – (-10) = 15 + 10 = 25 (м/с). То есть, за каждую секунду она прирастала на 25/5 = 5 м/с2 . Вот так. Тело двигалось равноускоренно с ускорением 5 м/с2 . Такому выводу соответствует график варианта ответа №3. Пример 4 задания А1 (взято из тренировочной работы от 30 апреля 2013 года)
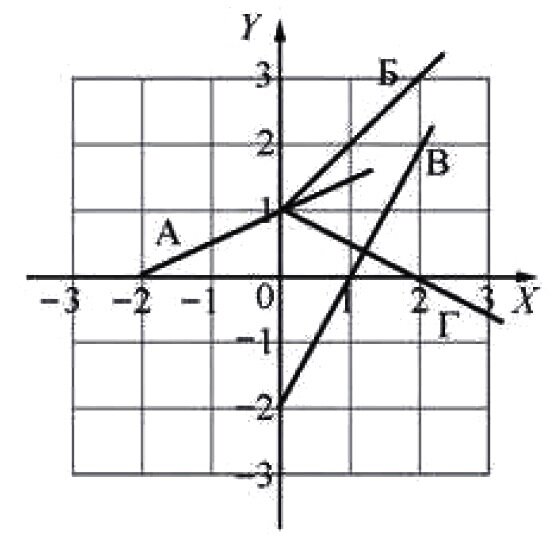
Зависимости координат от времени одного из этих тел имеют вид: Решение. В данном случае изображён не график, а следы, которые «прочертил» кораблик на поверхности моря. Зависимость координат от времени задана двумя функциями ( или лучше сказать – системой функций). А мы из алгебры знаем, что функция может быть задана тремя способами: аналитическим (формулой), табличным и графиком. Давайте-ка составим табличку зависимости икса и игрека от времени.
Вот так. А теперь надо найти прямую, которая проходит через точки с координатами 1,0; 2,2; 3,4; 4,6; 5,8. Легко заметить, что через 1,0; 2,2 проходит линия В. Ответ № 3. Пример 5 задания А1 (взято из пособия «Кабардин О.Ф. и др. Физика. ЕГЭ-2014»)
Через сколько секунд после начала отсчёта времени t = 0 c проекция вектора скорости тела на ось Ох станет равной нулю? Решение. Опять употреблен термин «проекции», но он нас нисколько не смущает. Скорость – помните? – можно находить, как производную от пути по времени. Поэтому первым шагом находим производную
А теперь – при каком времени t эта скорость станет равна нулю? То есть, по сути, мы составили уравнение, весьма несложное, с одним неизвестным t.
Решаем его
Пример 6 задания А2 (взято из пособия «В.А.Грибов ЕГЭ – 2014»)
Решение.
Если радиус увеличить в 3 раза, то ускорение уменьшится в 3 раза. Верный ответ № 2. <<< Назад I Вперед >>> |