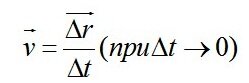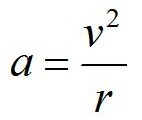|

Куда кривая вывезет…
20. В какую сторону направлен вектор скорости при криволинейном движении?
Мы только что рассматривали движение в трёхмерном пространстве, но это было ПРЯМОЛИНЕЙНОЕ движение. А теперь разберемся с особенностями криволинейного движения.
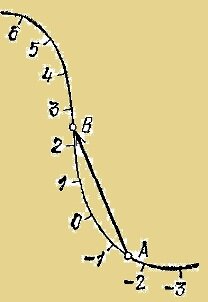
Траектория – кривая произвольной формы. Пройденный путь – это длина кривой траектории, вполне можно подсчитать. Скорость – тоже несложно, что касается величины (модуля) скорости. А вот направление? Куда направлен вектор скорости при криволинейном движении? При прямолинейном вектор скорости по направлению всегда совпадает с вектором перемещения. Так же и при криволинейном. Только надо иметь в виду, что вектор перемещения при криволинейном не совпадает с траекторией, он направлен по дуге (АВ на рисунке).
При очень малом перемещении 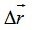 дуга АВ совпадёт с касательной к кривой в данной точке. А скорость мы определяем по формуле, где как раз употребляется очень малое перемещение. дуга АВ совпадёт с касательной к кривой в данной точке. А скорость мы определяем по формуле, где как раз употребляется очень малое перемещение.
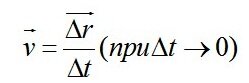
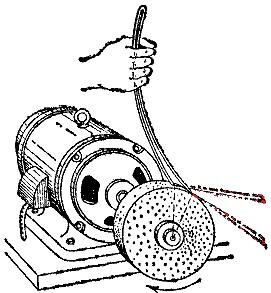
Значит, скорость также направлена по касательной к криволинейной траектории. Этот теоретический вывод мы нередко наблюдаем в жизни. Вот искры от точильного станка – летят по касательной. Грязь из-под колёс буксующего автомобиля – тоже по касательной.
21. А как быть с ускорением?
Сейчас мы сделаем очень интересный вывод, наглядно показывающий, что к векторам надо относиться совсем не так, как к скалярным величинам. Допустим некое тело (материальная точка) движется по окружности со скоростью 3 м/с. В любой точке движения скорость одинаковая – 3 метра в секунду. Каково ускорение этой точки?
- Никакого ускорения! – скажем мы. – Ускорение – это изменение скорости в единицу времени. А у нас скорость не изменяется, значит ускорение равно нулю.
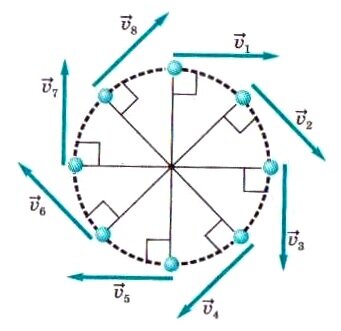
А если подумать хорошенько? По модулю скорость действительно не изменяется. А по направлению – посмотрите на рисунок – в каждой точке траектории направление вектора скорости другое. При переходе из одной точки в другую направление скорости изменяется! А – раз изменяется – значит, есть и ускорение!
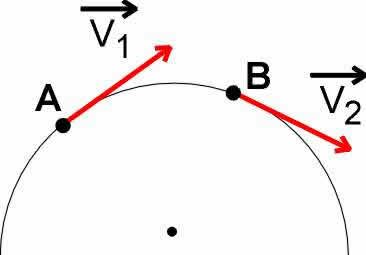
Проанализируем это дело потщательноее. Вот на рисунке показано направление скорости V1 в точке А и V2 в точке В.
Далее показано: для того, чтобы из вектора V1 получился вектор V2 (его мы перенесли параллельно самому себе в точку А, чтобы совмесимлись начала двух векторов), надо к V1 прибавить синенький вектор, направленный куда-то в сторону центра окружности.
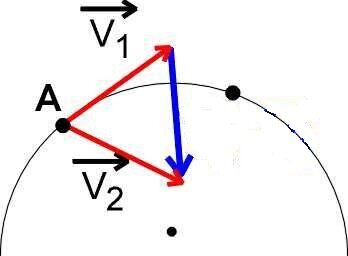
Таким образом при РАВНОМЕРНОМ (с постоянной скоростью) движении тела по окружности к его скорости всякий раз, при переходе от точки к точке, прибавляется добавочка 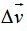 , благодаря которой получается уже иначе направленная скорость. А коли изменяется скорость – значит ускорение уже равно не нулю, а какому-то числу. И выходит, что это уже не равномерное, а равноускоренное движение. Путём геометрических построений доказывается, что это ускорение (совпадающее по направлению с добавочкой скорости , благодаря которой получается уже иначе направленная скорость. А коли изменяется скорость – значит ускорение уже равно не нулю, а какому-то числу. И выходит, что это уже не равномерное, а равноускоренное движение. Путём геометрических построений доказывается, что это ускорение (совпадающее по направлению с добавочкой скорости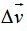 ) направлено строго по радиусу к центру окружности, как нарисовано на правой картиночке. Поэтому данное ускорение называют ЦЕНТРОСТРЕМИТЕЛЬНЫМ (стремится к центру окружности). ) направлено строго по радиусу к центру окружности, как нарисовано на правой картиночке. Поэтому данное ускорение называют ЦЕНТРОСТРЕМИТЕЛЬНЫМ (стремится к центру окружности).
22. Зависит ли центростремительное ускорение от скорости тела и от радиуса закругления траектории?
А зависит ли оно как - то от скорости движения тела и от радиуса круговой траектории? Должно зависеть. Можно даже вывести эту зависимость путём ощущений. Представьте – вы мчитесь по кругу. Чем больше ваша скорость – тем труднее свернуть. А от радиуса – обратно пропорционально – когда радиус маленький - повороты более крутые, а крутые повороты сложнее делать, чем пологие.

С помощью точных геометрических построений (которые мы пропускаем) выводится такая зависимость:
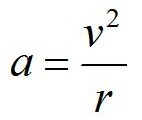
Обратите внимание, что речь здесь идёт только о модуле; а направлено ускорение к центру окружности.
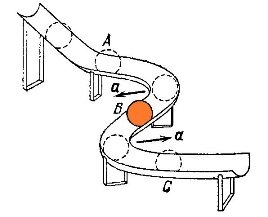
Центростремительное ускорение возникает не только при движении по окружности, но и вообще при любом криволинейном движении.
На рисуночке показан наклонный жёлоб, по которому скатывается шарик. В кривых участках шарик имеет центростремительное ускорение, направленное внутрь кривой.
|