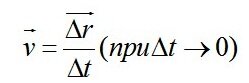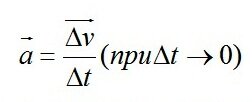|
Кораблик по морю плывёт, журавлик по небу летит….15. 3D
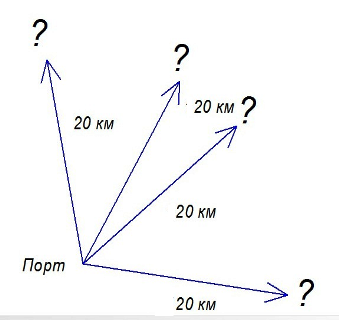
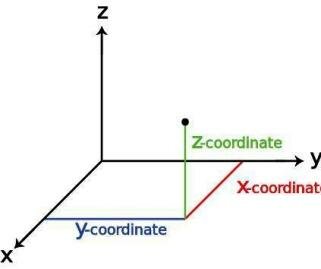
В отличие от поезда, который может двигаться только по линии, корабль может двигаться по поверхности (если, конечно, это не Титаник, тот может ещё и вниз). Местоположение корабля указывают двумя числами – широтой и долготой, по сетке параллелей и меридианов, как бы нанесённой на поверхности моря. Либо можно «привязать» к порту систему координат из двух перпендикулярных осей X и Y – и указать две координаты для местоположения корабля в море. Теперь уже будет не «точка отсчёта», как мы брали для поезда, а «система отсчёта».
Всё, о чём мы говорили в первом рассказе, относилось к движению тела вдоль прямой линии. И пройденный путь, и скорость, и ускорение. Такое движение на самом деле бывает, взять тот же поезд. Но оно – лишь частный случай движения вообще, которое может происходить в трёхмерном пространстве, и не по прямой, а по какой-нибудь кривой, дуге или вовсе по окружности. Сейчас мы такие движения и рассмотрим. Только для этого нам нужно ввести несколько новых понятий. 16. Чем отличаются путь и перемещение?
На первой – прямолинейная траектория взлетающего самолёта; на второй – криволинейная траектория автомобиля на извилистой дороге. На третьей – Вася вышел погулять, описал замысловатую траекторию, петляющую по району, а после прогулки вернулся домой.
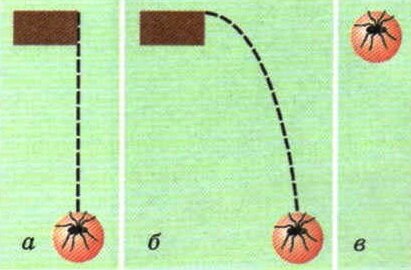
С точки зрения наблюдателя в вагоне – траектория – вертикальная прямая (а); с точки зрения человека на перроне – траектория кривая линия (б), складывающаяся из движения шарика вниз и движения вагона вправо; с точки зрения паучка, сидящего на шарике – шарик вообще не движется (в).
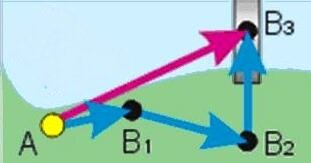
Если траектория кривая – как у автомобиля на извилистой дороге – то перемещение короче, чем путь. Если траектория замкнутая, как у гуляющего Васи, начало и конец в той же точке – то перемещение вообще равно нулю, никуда Вася в итоге своей прогулки не переместился. А если, как у взлетающего самолёта, траектория прямая и, на первый взгляд, путь и перемещение равны – всё равно есть разница. Перемещение – это ВЕКТОР. Вектором будем называть такую величину, которая характеризуется не только величиной (модулем), но и направлением. 17. Действия над векторами 1. Слагаемые векторы приставляем друг к дружке начало к концу, начало к концу . Тогда суммой всех этих векторов будет вектор, соединяющей начало первого с концом последнего. В самом деле, если бы Вася переместился сначала по вектору АВ1, отдохнул маленько, потом переместился по В1В2, ещё отдохнул, потом переместился В2В3, то в итоге три его перемещения были бы равноценны перемещению АВ3.
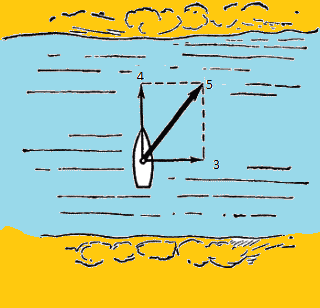
Мы, кстати, каждый день так перемещаемся, когда переходим перекрёсток по диагонали. По диагонали переходить улицу нельзя, вот мы и делаем два перпендикулярных перемещения, чтобы оказаться на диагонально противоположном углу. 2) Два вектора выходят из одной точки в разные стороны. Здесь хорошо представить лодочку, плывущую поперёк реки. Поперёк реки лодка совершает перемещение 4 метра. Но в это же самое время лодку сносит вниз по течению на 3 метра. Где же она окажется в итоге? Суммарный вектор – это диагональ прямоугольника, построенного на двух векторах-слагаемых. Направление её понятно, а модуль (длину) можно посчитать по теореме Пифагора. Такой способ сложения векторов называют «сложением по правилу параллелограмма» , потому что угол между векторами-слагаемыми не обязательно прямой, как на рисунке, а может быть, в принципе, любым.
Довольно легко вывести правило умножения вектора на число, если представить сложение нескольких равных векторов, направленных в одну сторону. Правило будет такое: при умножении (делении) вектора на число его модуль увеличится (уменьшится) в несколько раз, а направление останется тем же самым. 18. Получается, скорость и ускорение – тоже векторы?
Скорость – это отношение перемещения к промежутку времени, в течение которого это перемещение произошло. Раз перемещение – вектор, а время – скаляр, то есть просто число, то мы имеем действие деления вектора на число. В результате получится вектор, направленный в ту же сторону, что и делимое. То есть, скорость – это вектор, направление которого совпадает с направлением вектора перемещения.
И направлено оно, получается, в ту же сторону, что и скорость. 19. А теперь – наёборот!
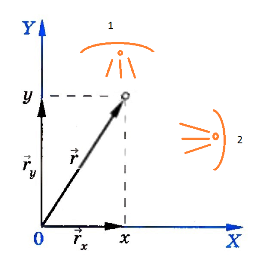
Вот мы нарисовали две лампочки с отражателем и лучиками света. Допустим тело (материальная точка) движется по вектору перемещения <<< Назад I Вперед >>> |