|

Степени, корни, логарифмы
Он очень образованный, он постиг четыре действия арифметики! – восклицал один литературный герой, если не ошибаюсь, Старик Хоттабыч, говоря про своего друга Вольку.
Мы тоже знаем эти действия: сложение, вычитание, умножение и деление.
Но шагнем дальше и добавим в свой интеллектуальный багаж ещё три действия:
- возведение в степень;
- извлечение корня;
- нахождение логарифма.
Эти три действия очень сильно связаны между собой.
Возведение в степень
Например, есть такое умножение: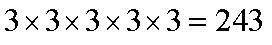
Тройка пять раз умножена сама на себя, или, если выразиться математически правильно, взята сомножителем 5 раз. В этом случае говорят: «Число 3 возведено в 5-ую степень». Записывают так:
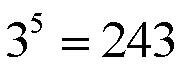
Тройка называется основанием степени, а пятерка (она поменьше размером и пишется сверху) называется показателем степени. Значит: возвести число в степень – это взять основание степени сомножителем столько раз, каков показатель степени. Например
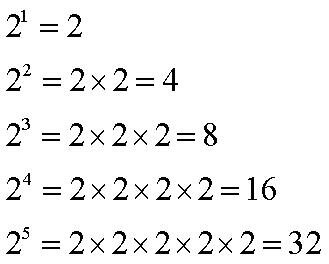
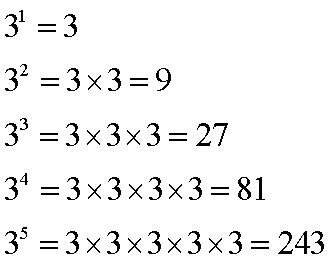
Не поленитесь, напишите еще столбики для других оснований степени (особенно полезно, если напишите и постараетесь запомнить вторые степени для чисел второго десятка – 11, 12, 13, 14, 15)
Для чего же может пригодиться действие возведения в степень? Например, требуется найти площадь квадрата, сторона которого равна 4 м.
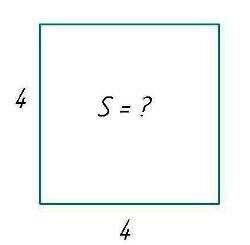
Его площадь 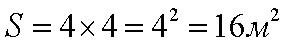
Это весьма распространенная задача, поэтому говорят не «четыре во второй степени», а «четыре в квадрате»; не «возвести во вторую степень», а «возвести в квадрат».
А как найти объем бака, имеющего форму куба?
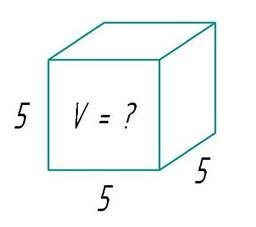
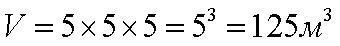
Третью степень так и называют – «кубом», и говорят «пять в кубе».Остальные степени собственных названий не имеют, называются просто числом. Любое число в 1-ой степени – есть само это число.
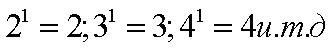
Поэтому число 1 в показателе степени не пишется, а только подразумевается.
Две противоположности
Действие сложение имеет противоположное действие вычитание. Действие умножения имеет противоположное действие деление.
А есть ли противоположности у действия возведения в степень?
Есть! И не просто есть, а есть целых две противоположности.
Как это? Давайте разберемся.
Напишем еще раз: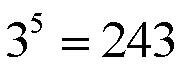 А теперь возьмем кусочек бумаги и будем поочередно закрывать каждое из трех чисел. А теперь возьмем кусочек бумаги и будем поочередно закрывать каждое из трех чисел.
1. 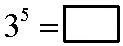 Вопрос: сколько будет 3 в пятой степени? Ответ на этот вопрос дает действие возведения в степень 3 в 5-ой степени = 243 Вопрос: сколько будет 3 в пятой степени? Ответ на этот вопрос дает действие возведения в степень 3 в 5-ой степени = 243
2.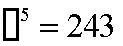 Вопрос: какое число, возведенное в пятую степень, будет равно 243? Ответ на этот вопрос дает действие извлечения корня Вопрос: какое число, возведенное в пятую степень, будет равно 243? Ответ на этот вопрос дает действие извлечения корня 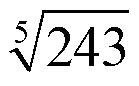
3. 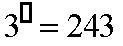 Вопрос: в какую степень надо возвести число 3, чтобы получилось 243? Ответ на этот вопрос дает действие нахождения логарифма Вопрос: в какую степень надо возвести число 3, чтобы получилось 243? Ответ на этот вопрос дает действие нахождения логарифма 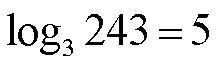
Таким образом, мы выяснили, что эти три действия очень тесно связаны между собой. КОРНИ и ЛОГАРИФМЫ – это два действия, противоположные СТЕПЕНИ.
Корни
Итак, обратимся к корню. Корень изображается так: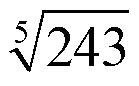
Сам значок  называют «знаком корня» или «радикалом». Число 5, стоящее на полочке радикала, называют «показателем корня», число 243 – «подкоренным».Извлечь корень n-ой степени из какого-то числа a – это значит найти такое число, которое будучи возведенным в n-ую степень, станет равно a. называют «знаком корня» или «радикалом». Число 5, стоящее на полочке радикала, называют «показателем корня», число 243 – «подкоренным».Извлечь корень n-ой степени из какого-то числа a – это значит найти такое число, которое будучи возведенным в n-ую степень, станет равно a.
Мы рисовали список степеней с основаниями 2 и 3; можно сделать аналогичный список для корней.
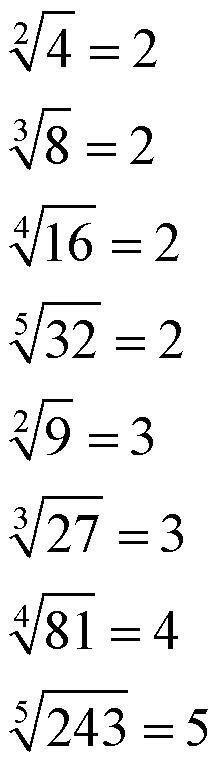
К действиям извлечения корня приводит практическая задача нахождения стороны квадрата по его площади. Пусть площадь квадрата 64 кв.м. Тогда его сторона
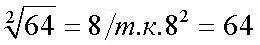
Потому корень второй степени принято называть «квадратным корнем». Для квадратного корня показатель корня 2 не пишется, а подразумевается. Поэтому следовало написать не 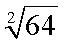 ,а просто ,а просто 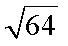 .Задача – найти сторону бака кубической формы по известному объему – приводит к извлечению корня третьей степени. .Задача – найти сторону бака кубической формы по известному объему – приводит к извлечению корня третьей степени.
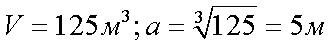
Корень третьей степени принято называть «кубическим корнем», но здесь число 3 в показателе корня пишется.
Остальные корни называются просто: корень четвертой, пятой, шестой степени и так далее.
А как вообще-то вычислять корни? Со степенями было понятно – там надо было много раз умножать число само на себя. А с корнями? Обычно в ЕГЭ встречаются небольшие число под знаком корня и небольшие показатели корня. Такие мы должны помнить наизусть, как таблицу умножения. А если забыли – поприкидывайте, поподбирайте, исходя из определения корня.
Ну а сложные корни (большие показатели, большие подкоренные числа) считают с помощью инженерных калькуляторов или таблиц.
Логарифмы
Пишется так: 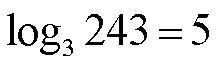
Говорится так: «логарифм по основанию 3 от числа 243». Тройка (маленькая и пишется чуть ниже) называется «основанием логарифма», а число 243 так и называют «числом». Найти логарифм – это значит найти показатель степени, в которую надо возвести основание логарифма, чтобы получить стоящее под логарифмом число.
Примеры: Логарифмы по основанию 2
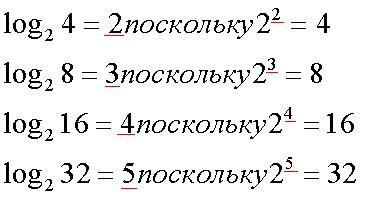
Логарифмы по основанию 3
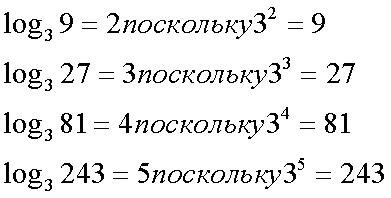
Продолжение теории "Степени, корни, логарифмы"
|
![]()


