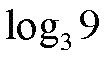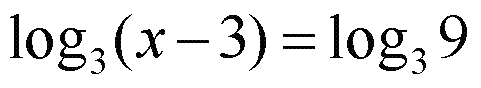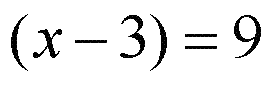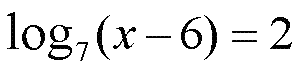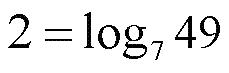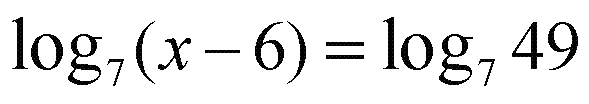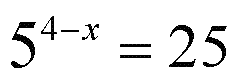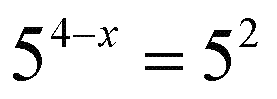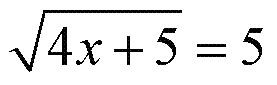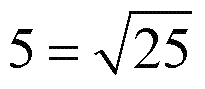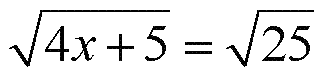Добавить свое объявление
Загрузка...

Задача В5 Уравнения

 

Пару слов ДО того...

Если Вы отлично представляете

  • что такое уравнение, каковы его свойства, что значит "решить уравнение"
  • как решаются алгебраические уравнения, в том числе квадратные
  • как решаются простейшие показательные уравнения (хотя бы - какие они вообще - показательные)
  • как решаются простейшие логарифмические уравнения
  • как решаются иррациональные уравнения (которые с квадратными корнями)

тогда смело беритесь за разбор наших примеров. Если представляете ТУМАННО, то сначала настоятельно рекомендую почитать нашу теорию к задаче В5 про уравнения (по этой ссылке)

Пример В5 - 1 (Из демоварианта 2013 года)

Задание В5 ЕГЭ по математике

Решение:

Вспоминаем определение логарифма: ЛОГАРИФМ - это есть ПОКАЗАТЕЛЬ СТЕПЕНИ, в которую надо возвести ОСНОВАНИЕ, чтобы получить ЧИСЛО. Вспомнив это, мы правую часть уравнения можем представить в следующем виде.

То есть тройка в квадрате - это девять. Поэтому вместо числа 2 мы вполне можем вставить равное ему выражение. И тогда наше уравнение превратится вот в такое

А здесь - в каждой части уравнения стоит одинаковый значок логарифма, одинаковое основание - тройка, значит мы имеем полное право приравнять и те выражения, которые стоят после логарифма (или, как говорят, под знаком логарифма)

ЕГЭ по математике Задача В5

А это уже простецкое алгебраическое уравнение. Переносим тройку в правую часть с противоположным знаком, с плюсом, складываем с девяткой и получаем ответ 12.

Посмотрим видео о решении данной задачки:

Пример В5 - 2

Найдите корень уравнения ЕГЭ по математике Задание В5

Задание точно такое же, я привел его для закрепления

ЕГЭ по математике Задачка В5 на логарифмы

ЕГЭ по математике Задание В5

А теперь легко и непринужденно находим X - 6 = 49; X= 49 + 6 = 55

Пример В5 - 3

Найдите корень уравнения ЕГЭ по математике Задание В5

Это уже несколько другое, так называемое ПОКАЗАТЕЛЬНОЕ уравнение. Оно так называется, потому что неизвестная величина ИКС стоит в ПОКАЗАТЕЛЕ СТЕПЕНИ. Но решается почти также. Мы быстренько соображаем, что 25 это 5 в квадрате. И записываем уравнение в таком виде

ЕГЭ по математике Задача В5

А дальше рассуждаем так. Раз основания степеней равны, и там и там пятерка, то мы вправе приравнять и показатели степени. То есть зафигачим вместе этого такое простецкое уравнение 4 - x = 2 откуда х = 4 - 2 = 2

Пример В5 - 4

Найдите корень уравнения ЕГЭ по математике Задача В5

Такое уравнение, когда неизвестная величина ИКС стоит под знаком корня, называется ИРРАЦИОНАЛЬНЫМ (кто научится выговаривать это слово - уже большой молодец!)
Будем его решать таким же типовым способом, как и предыдущие задачи. Сперва смекнем, что

ЕГЭ по математике

Потом исходное уравнение перепишем в таком виде

ЕГЭ по математике

А затем повторим те же самые рассуждения: раз и в левой и в правой части стоят одинаковые корни, то имеем право приравнять и подкоренные выражения, откуда 4x + 5 = 25; 4x = 25 - 5 = 20; x = 20/4 = 5

 

Назад к задаче В4 /Задача В5/ Вперед к задаче В6

загрузка...