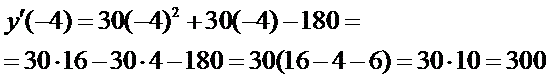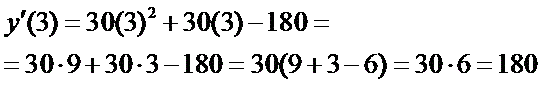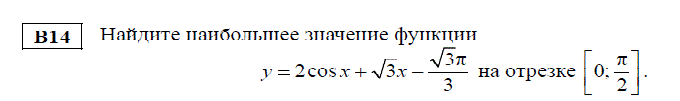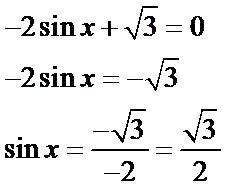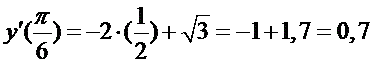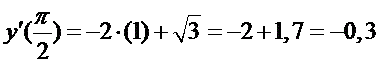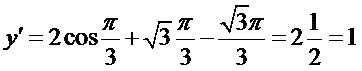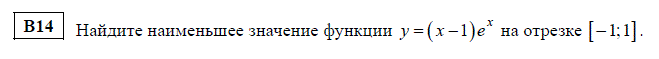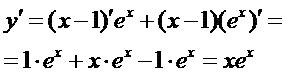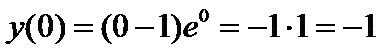Для решения этой задачки надо знать две темы:
Насчёт производных - ну, надо их знать, если не знаешь - не фиг и браться за задчку В14, производные в ней главное. Так то, производные не сильно сложная штука. Надо просто запомнить таблицу производных (как в первом классе таблицу умножения) - и всё, проблем нет! Кто подзабыл - ПОЧИТАЙТЕ ВОТ ЭТУ СТРАНИЧКУ НА НАШЕМ САЙТЕ. А про вторую тему маленько поговорим. С помощью производной функцию можно ИССЛЕДОВАТЬ НА ВОЗРАСТАНИЕ И УБЫВАНИЕ. Помните геометрический смысл производной?
Функция, как мы знаем, может или возрастать, или убывать. Если график идёт снизу вверх (от левого нижнего к правому верхнему углу) – то функция возрастает. Если сверху вниз – функция убывает.
Для убывающей функции касательная (зеленый цвет) составляет с осью абсцисс тупой угол, значит тангенс и производная отрицательна.
Так вот, друзья мои, задача В14 построена так. Дана формула какой-нибудь функции. И спрашивается: найдите или наибольшее, или наименьшее значение этой функции на таком-то участке. Решается эта задача по следующему плану.
Ну, давайте примерчик. Пример В14 – 1
Решение. Шаг уан - находим производную Шаг ту - приравниваем производную к нулю, получится уравнение с неизвестным иксом.
Уравнение не изменится, если обе его части разделить на одно и то же число. Такое свойство мы учили в шестом классе. Разделим на 30, чтобы числа были поменьше и решать его было полегче.
Ну и решаем. Это квадратное уравнение, решать его надо - помните? - с дискриминантом. Кто забыл - почитайте теорию тут.
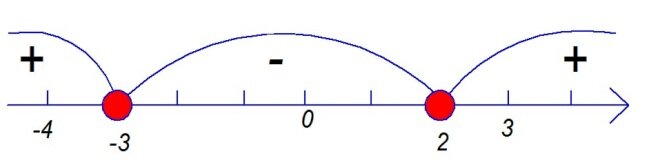
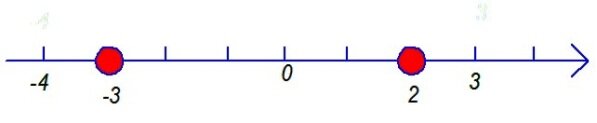
Вот, получили два корня, две точки, В этих точках график функции имеет перегиб. Только - в которой максимум, а в которой минимум - пока не понятно. Шаг третий - найдем знак производной до и после этих критических пергибных точек. Например, левее, чем минус три - возьмём минус 4. Между ними - ноль. Правее, чем 2 - три.
Производная положительна!
Производная отрицательна!
Производная опять положительна! Обычно рисуют такую схемку:
До минус 3 производная была положительна, функция возрастала. После - убывала, потому что производная отрицательна. С возрастания перегнулась на убывание - значит это был МАКСИМУМ в точке -3. А в точке 2 ,наоборот, с убывания на возрастание, значит это был МИНИМУМ. В условии просят найти МИНИМУМ - это в точке 2. А шага четвёртого здесь не будет. Если бы просили найти значение ФУНКЦИИ в точке минимума - тогда бы нужен был шаг четвёртый. Здесь достаточно найти "точку минимума" то есть значение икс. Мы его и нашли. Ответ 2. Пример В14-2(Это из демоварианта 2013 года)Предыдущий пример был довольно лёгкий. Потому что надо было найти производную от суммы степенных функций. Это обычно все умеют. А встретится функция посложнее - вот уже и тупят. Разберем более хитрый примерчик.
Соственно говоря, особой хитрости тут нет, просто взята тригонометрическая функция КОСИНУС, она кой-кого, шарахающегося от тригонометрии, может напрягать.
Шаг второй. Приравниваем производную к нулю и решаем полученное уравнение.
Это прям-таки табличное значение! Если синус равен корень из трёх на два - то это угол 60 градусов, Шаг третий. Итак, мы установили, что в точке
Здесь корень из трех я очень грубо округлил до 1,7 - но, тем не менее, ясно, что производная ПОЛОЖИТЕЛЬНА, значит функция ВОЗРАСТАЕТ. А теперь от 90 градусов. Синус 90 градусов равен 1, как мы помним...
Производная отрицательна, функция убывает. Значит, она сперва возрастала, потом стала убывать. Это говорит о том, что в точке перегиба она имела МАКСИМУМ. Найдено!!! Но в данной задаче требуется ШАГ ЧЕТВЁРТЫЙ - потому что требуется найти наибольшее значение функции, то еасть ИГРЕКА. Для этого найденный максимум икса
Всё сосчиталось очень здорово! Второй и третий член с разными знаками взаимно уничтожились. Косинус 60 градусов равен 1/2. Таким образом, наибольшее значение функции 1. Это ответ, который надо вписать в бланк ЕГЭ. Пример В14-3 (Это уже из демоварианта 2014 года)
Шаг первый - находим производную. Этот шаг здесь не самый простецкий. Отмечаем, что дано произведение двух функций. Одна
От первой функции производная равна 1. А вторая функция - своеобразная, она называется экспонента, и своеобразие её в том, что производная её такая же, как и сама функция
Шаг второй - приравниваем производную к нулю и решаем полученное уравнение. Можно подумать, что это уравнение довольно замысловатое
На самом деле оно весьма простое. Шаг третий. Выясняем, какой перегиб в точке х = 0 МАКСИМУМ ИЛИ МИНИМУМ? Выбираем два значения х = - 1 и х = 1. При х = - 1 производная отрицательна, при х = 1 положительна. Значит в точке х = 0 функция имеет МИНИМУМ. Шаг четвертый - находим значение функции в этой точке
Это и есть ответ - наименьшее значение функции. Вот ролик с you tube о решении задачи В14. Очень подробный. Если весь просмотришь - будешь молоток...
|




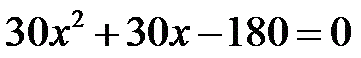
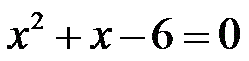
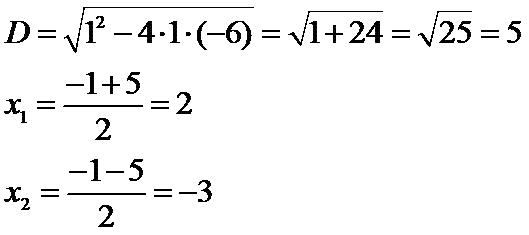
 ,
,