
|
ЕГЭ МАТЕМАТИКА 2017
ДЕМО
Профильный уровень
Работа включает в себя 19 заданий. Прикинь: в базовом 20, а в профильном 19!
- 8 заданий базового уровня сложности, при решении которых достаточно привести краткий ответ;
- 4 задания повышенного уровня сложности, тоже с кратким ответом;
- и 7 заданий высокого (но не запредельно высокого!) уровня сложности, где должен быть записан развёрнутый ответ, то есть - ход решения
|
Сколько задачек из девятнадцати надо научиться решать?
- Если ЕГЭ нужен только для аттестата, то вообще-то надо сдавать не профильный, а базовый. Но вдруг ты протупил по какой-то причине и выбрал профильный - то решай только задания с 1 по 8, для аттестата хватит.
- Если ты поступаешь в технический ВУЗ на инженерную специальность, то тебе нужно уверенно решать 16 заданий, а именно с 1 по 15 плюс 17.
- Если ты поступаешь на "физмат" или на экономику в престижном универе, где принимают стобалльников - то учись уверенно решать все 19 заданий!
|
|
|
Поезд отправился из Санкт-Петербурга в 23 часа 50 минут (время московское) и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?
|
|
|
Сутки - это 24 часа. Начало суток 0 - 00. Ночь. Время пошло: 1-00, 2-00, 3-00 итд. В 12-00 стрелки часов встали на то же место, что и в начале суток. Но - прошло только 12 часов, только половина суток. Потом 13-00, 14-00, 15-00 и так далее. Наконец, 22-00, 23-00, 23-57, 23-58, 23-59 и далее.... сколько? Можно сказать 24-00, а можно сказать 0-00 следующих суток.
Простите, за такое дурацкое изложение, это, конечно, всем известно.
Теперь о задаче. Поезд отправился в 23-50. Прошло всего 10 минут, как наступили следующие сутки. А в следующие сутки поезд был в пути 7 часов 50 минут. То есть, всего он был в пути 7-50 + 10 минут = 8 часов.
|
|
|
8 |
|
|
На рисунке точками показана средняя температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Для наглядности точки соединены линией.
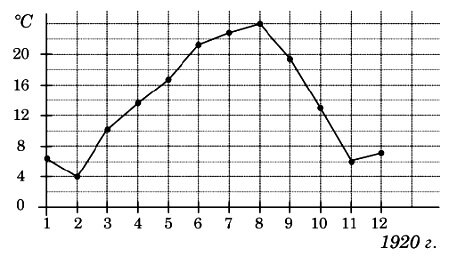
Определите по рисунку, сколько месяцев из данного периода средняя температура была больше 18 градусов Цельсия.
|
|
|
Достаточно мысленно провести горизонтальную линию по отметке 18 градусов. Само число 18 на оси температур не показано, но видно, что цена деления оси 2 градуса, то есть 18 будет посередине между 16 и 20. Мы видим, что четыре месяца 6; 7; 8 и 9 лежат выше этой линии. Обратите внимание: в условии сказано, что точки "для наглядности" соединены линией, сама по себе линия ничего не обозначает, числовое значение имет только точки.
|
|
|
4 |
|
|
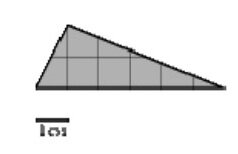
На клетчатой бумаге с размером клетки 1см х 1см изображён треугольник. Найдите его площадь. Ответ дайте в квадратных сантиметрах.
|
|
|
Площадь треугольника равна половине произведения основания на высоту. Длина основания 6 см. Высота 2 см. Площадь 1/2 х 6 х 2 = 6
|
|
|
6 |
|
|
В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах. |
|
|
Делают некий ОПЫТ. Это термин такой в теории вероятностей. В нашей задачке опыт – вытягивание билета из сборника. У этого опыта возможно сколько-то ИСХОДОВ. В нашей задачке – возможно 25 исходов.
То есть, исход № 1 – это попался билет № 1; исход № 2 – попался билет № 2 и так далее, всего 25 исходов.
СОБЫТИЕ (А), которого мы ожидаем, состоит в том, что в вытянутом нами билете есть вопрос о грибах. Этому событию БЛАГОПРИЯТСТВУЮТ (приводят к нему) 2 из 25 исходов, а в двух исходах данное событие не наступит (вопрос о грибах всё-таки попадётся!).
Вероятностью события А называется отношение числа m исходов, благоприятствующих событию А, к общему числу n исходов данного опыта.
P(A)= m / n
В нашем случае m = 2, n= 25, P(A) = 2/25 = 0,08
|
|
|
0,08 |
|
|
Найдите корень уравнения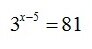 |
|
|
Это так называемое "показательное уравнение", когда неизвестная величина х в показателе степени. Как решать?
Число 81 представим, как
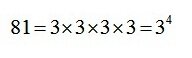
тогда исходное уравнение можно переписать в таком виде
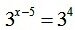
А дальше понятно - основания степеней одинаковые в правой и левой части, тройки, между частями знак "равно", следовательно можно приравнять и показатели степени
х - 5 = 4, отсюда х = 4 + 5 = 9
|
|
|
9 |
|
|
Треугольник ABC вписан в окружность с центром O. Угол BAC равен 32 .° Найдите угол BOC . Ответ дайте в градусах. |
|
|
Угол ВАС называется ВПИСАННЫМ углом. У него вершина А лежит на окружности. Угол ВОС называется ЦЕНТРАЛЬНЫМ. Его вершина лежит в центре окружности.
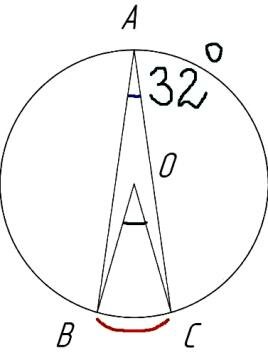
А теперь ВНИМАНИЕ! Есть свойства вписанного и центрального угла, которые обязательно надо знать для решения данной задачки. Центральный угол (в градусах) равен дуге, на которую он опирается. Вписанный угол равен ПОЛОВИНЕ градусов дуги, на которую он опирается.
В нашем случае и тот и другой угол опираются на одну и ту же дугу. Угол ВАС равен 32 градуса, а угол ВОС, следовательно, в два раза больше, то есть 64 градуса.
|
|
|
64 |
|
|
На рисунке изображён график дифференцируемой функции y = f (x). На оси абсцисс отмечены девять точек: х1, х2, х3, ... х9 .
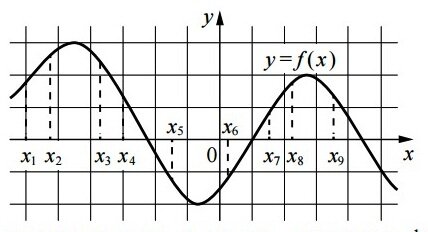
Найдите все отмеченные точки, в которых производная функции f (х ) отрицательна. В ответе укажите количество этих точек.
|
|
|
Надо вспомнить графический смысл производной.
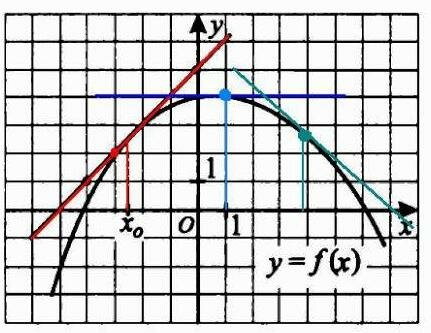
Производная численно равна тангенсу угла наклона касательной. Если функция возрастает, касательная составляет с осью ОХ острый угол (красный цвет), производная положительна. Если функция убывает, касательная составляет с осью ОХ тупой угол (зелёный цвет), производная отрицательна. Если график функции в точке перегиба, касательная параллельна оси ОХ (синий цвет), производная равна нулю.
На рисунке в задании функция убывает в точках х3, х4, х5 и х9. То есть четыре точки
|
|
|
4 |
|
|
В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором сосуде? Ответ выразите в см |
|
|
Объём цилиндра равен площади основания, умноженной на высоту.
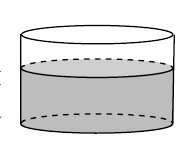
А площадь круглого основания равна "пи эр квадрат".
Итак, давайте запишем объёмы первого и второго цилиндров в буквенном виде (точнее говоря, не объём сосудов, а объём воды в сосудах).
.jpg)
И поскольку в первом и втором сосуде та же самая вода (V1=V2), приравняем правые части этих формул
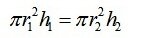
А дальше, во-первых для простоты сократим на "пи", а во-вторых вместе r2 запишем согласно условию 4r1(В условии дано, что диаметр второго цилинда больше первого в два раза. Но ведь диаметр - это два радиуса, значит радиус второго цилиндра в 4 раза больше).
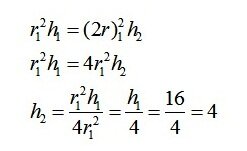
|
|
|
4 |
|
|
|
|
![]()












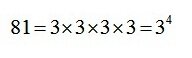







.jpg)
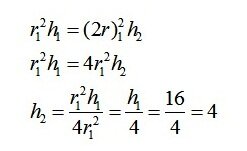
.gif)





