|
Для примера приводим одну главку из этой книг.
КРЕСТИКИ—НОЛИКИ, ИЛИ ТИК-ТАК-ТОУ
— Ну, это так же просто, как сыграть в крестики—нолики,
и так же легко, как не учить уроков.
По-моему, мы могли бы придумать способ хоть капельку посложней, Гек Финн.
Марк Твен. Приключения Гекльберри Финна
Тик-так-тоу, или игра в крестики — нолики, вовсе не так проста, как это казалось Тому Сойеру. Когда Ч. С. Пирс писал свою книгу «Элементы математики», он посвятил целых 17 страниц анализу только начального этапа этой древней игры, что, кстати, явилось одним из многих предвидений «современной математики», обнаруженных Пирсом. Сейчас многие преподаватели новой формации часто обращаются к игре в крестики-нолики, когда знакомят своих учеников с такими математическими понятиями, как взаимное пересечение множеств, симметрия вращения, зеркальная симметрия, евклидово пространство более высокой размерности и т. д. В этой главе мы рассмотрим некоторые необычные аспекты этой игры, обсуждение которых не вошло в мои предыдущие книги.
Традиционная игра в крестики — нолики, как, наверное, знает большинство наших читателей, при условии оптимальной стратегии каждого из игроков должна обязательно заканчиваться вничью.
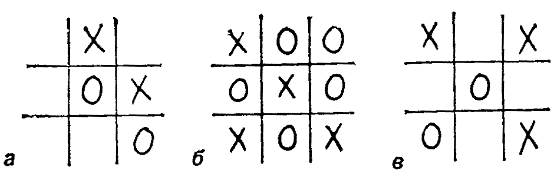
Рис. 49. Игра в крестики и нолики: три простые позиции.
Различные забавные задачки, связанные с игрой в крестики — нолики, довольно часто появляются в рекламных текстах или в иллюстрированных журналах. Например, в нью-йоркской газете Herald Tribune (May 13, 1956) была напечатана реклама фирмы ИБМ с незаконченной позицией, возникшей при игре в крестики — нолики (рис. 49, а). Кто из игроков начинал в этом случае партию, если считать, что оба они не совершали глупых ходов? Не требуется больших усилий, чтобы догадаться что игрок, ставящий нолики, не мог начинать игру, поскольку в этом случае его партнер своим вторым ходом поставил бы крестик в верхней левой клетке. Остальные две позиции почти так же тривиальны. Возможна ли, например, позиция, показанная на рис. 49, б? Она взята из газеты The Saturday Evening Post (January 16, 1937). Позиция на рис. 49, в тоже заимствована из рекламного текста (The New York Times, June 1, 1971); кстати, какой ход был сделан здесь последним?
Если первый игрок, скажем X, начинает игру с центральной клетки, то он легко может свести партию к ничьей, которая, вообще говоря, всегда заканчивается одной и той же финальной позицией. На этом основано несколько трюков с предсказанием ходов. Например, демонстратор на квадратном листочке бумаги рисует окончательную позицию партии со всеми заполненными клетками. Затем он переворачивает листок, не показывая его окружающим. После этого он разыгрывает партию с кем-либо из присутствующих на другом листочке бумаги. Как только игра заканчивается вничью, он переворачивает листок со своим «прогнозом» и — о, чудо! — оба рисунка в точности повторяют друг друга.
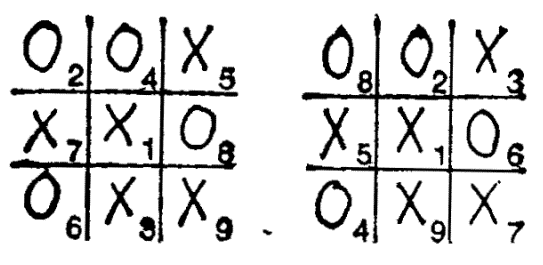
Рис. 50. Фокус с предсказанием
На рис. 50 показано, как это делается. Предположим, игрок X начинает партию ходом в центр.
Если его партнер 0 делает ход в любую из угловых клеток, то Х сразу сводит игру к ничьей в позиции, показанной на рисунке (цифры обозначают здесь последовательность ходов).
При этом игрок X должен четко представлять только одно — куда сделать свой второй ход, поскольку все его последующие ходы обусловлены именно этим вторым ходом. Для запоминания второго хода можно предложить следующее простое правило: игрок X выбирает угловую клетку, противоположную первому ходу игрока 0, после чего занимает клетку, лежащую рядом с ней в направлении движения часовой стрелки. Если же игрок 0 своим первым ходом занимает одну из боковых клеток, то его партнер сразу же сводит игру к ничьей с помощью позиции, показанной справа. В такой ситуации вынужденные ходы делает только игрок 0, а X должен лишь держать в голове следующие четыре хода. Для этого подходит простое правило: игрок X делает свой второй, третий и четвертый ходы на клетки, соседние с предшествующими ходами игрока 0 и лежащие от них в направлении движения часовой стрелки, а свой пятый ход — на единственную оставшуюся свободной клетку. Это правило было предложено неким Торсоном и опубликовано в журнале М. I). M. (September 1960), официальном органе Общества американских фокусников.
Обратите внимание, что обе финальные позиции здесь совпадают. Само собой разумеется, что каждая полученная позиция может быть ориентирована по отношению к «прогнозу» четырьмя различными способами (т. е. оказаться повернутой на 90, 180 или 270°), однако в таком случае фокусник как бы невзначай поворачивает листок с предсказанием в нужное ему положение и получает картинку, в точности повторяющую изображение только что законченной партии.
ОГЛАВЛЕНИЕ
От переводчика
Введение
Глава 1. Колеса
Глава 2. Диофантов анализ и большая теорема Ферма
Глава 3. Молекула с узлами и другие задачи
Глава 4. Иерархия алефов и сверхзадачи
Глава 5. Нетранзитивная игра в кости и другие парадоксы теории вероятностей
Глава 6. Геометрические заблуждения
Глава 7. Комбинаторика складывания бумаги
Глава 8. Набор простеньких задач
Глава 9. Крестики — нолики, или тик-так-тоу
Глава 10. Складывание многогранников
Глава 11. Игра хальма
Глава 12. Рекламные призы
Глава 13. Сэлмон о собаке Остина
Глава 14. Ним и Хакенбуш
Глава 15. Изящные графы Голомба
Глава 16. Лыжник Чарлза Адамса и другие задачи
Глава 17. Шахматные задания
Глава 18. Ползунок, 3Х + 1 и другие любопытные вопросы
Глава 19. Математические фокусы с картами
Глава 20. Игра «Жизнь». Часть I
Глава 21. Игра «Жизнь». Часть II
Глава 22. Игра «Жизнь». Часть III
Литература
|